Advertisements
Advertisements
प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC such that DE║BC
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.

उत्तर
In Δ ABC, it is given that DE ∥ BC.
Applying Thales’ theorem, we get:
`(AD)/(DB)=(AE)/(EC)`
∵ AD = 3.6 cm , AB = 10 cm, AE = 4.5cm
∴ DB = 10 − 3.6 = 6.4cm
Or,` 3.6/6.4=4.5/(EC)`
Or, EC =`( 6.4×4.5)/3.6`
Or, EC= 8 cm
Thus, AC = AE + EC
= 4.5 + 8 = 12.5 cm
APPEARS IN
संबंधित प्रश्न
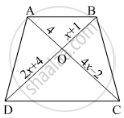
In below figure, If AB || CD, find the value of x.
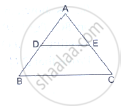
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
What values of x will make DE || AB in the given figure?

In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
