Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
उत्तर
Given: A quadrilateral ABCD where ∠A + ∠D = 90°.
To prove: AC2 + BD2 = AD2 + BC2
Construction: Extend AB and CD to intersect at O.
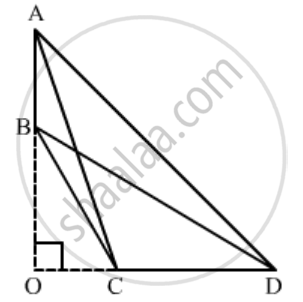
Proof:
In ΔAOD, ∠A + ∠O + ∠D = 180°
⇒ ∠O = 90° [∠A + ∠D = 90°]
Apply Pythagoras Theorem in ΔAOC and ΔBOD,
AC2 = AO2 + OC2
BD2 = OB2 + OD2
∴ AC2 + BD2 = (AO2 + OD2) + (OC2 + OB2)
⇒ AC2 + BD2 = AD2 + BC2
This proves the given relation.
APPEARS IN
संबंधित प्रश्न
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In the given figure, DE || BD. Determine AC and AE.

In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
