Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
उत्तर
Given: A quadrilateral ABCD where ∠A + ∠D = 90°.
To prove: AC2 + BD2 = AD2 + BC2
Construction: Extend AB and CD to intersect at O.
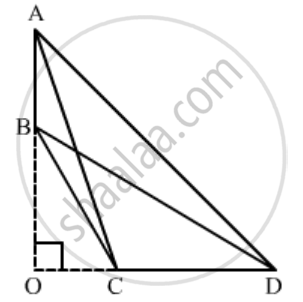
Proof:
In ΔAOD, ∠A + ∠O + ∠D = 180°
⇒ ∠O = 90° [∠A + ∠D = 90°]
Apply Pythagoras Theorem in ΔAOC and ΔBOD,
AC2 = AO2 + OC2
BD2 = OB2 + OD2
∴ AC2 + BD2 = (AO2 + OD2) + (OC2 + OB2)
⇒ AC2 + BD2 = AD2 + BC2
This proves the given relation.
APPEARS IN
संबंधित प्रश्न
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In ∆ABC, ∠ABC = 135°. Prove that AC2 = AB2 + BC2 + 4 ar (∆ABC)
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
