Advertisements
Advertisements
Question
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
Solution
Given: A quadrilateral ABCD where ∠A + ∠D = 90°.
To prove: AC2 + BD2 = AD2 + BC2
Construction: Extend AB and CD to intersect at O.
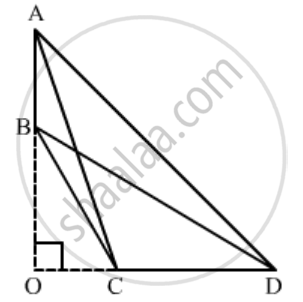
Proof:
In ΔAOD, ∠A + ∠O + ∠D = 180°
⇒ ∠O = 90° [∠A + ∠D = 90°]
Apply Pythagoras Theorem in ΔAOC and ΔBOD,
AC2 = AO2 + OC2
BD2 = OB2 + OD2
∴ AC2 + BD2 = (AO2 + OD2) + (OC2 + OB2)
⇒ AC2 + BD2 = AD2 + BC2
This proves the given relation.
APPEARS IN
RELATED QUESTIONS
What values of x will make DE || AB in the given figure?

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
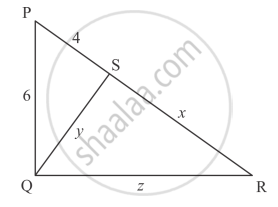
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
