Advertisements
Advertisements
Question
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
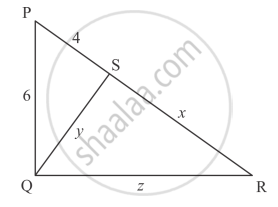
Solution
Δ PQR is a right triangle, right angled at Q
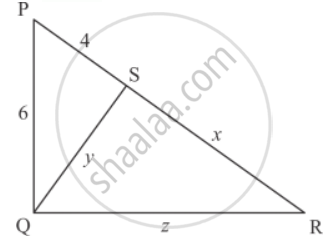
`6+z^2 = (4+x)^2`
`6+z^2=16+x^2+8x`
`z^2-x^2-8x=16-36`
`z^2-x^2-8x=16-36`
`z^2-x^2-8x=-20`......(1)
Δ QSP is a right triangle right angled at S
`QS^2+PS^2=PQ^2`
`y^2+4^2=6^2`
`y^2+16=36`
`y^2=36-16`
`y^2=20`
`y=sqrt20`
`y=sqrt(2xx2xx5)`
`y=2sqrt5`
Δ QSR is a right triangle right angled at S
`QS^2+RS^2=QR^2`
`y^2+x^2=z^2`..........(2)
Now substituting `y^2+x^2=z^2` in equation (i) we get
`y^2+x^2-x^2-8x=-20`
`20-8x=-20`
`-8x=-20-20`
`-8x=-40`
`x=40/8`
`x=5`
Now substituting ` x = 5` and `y^2=20` in equation (ii) we get
`y^2+x^2=z^2`
`20+5^2=z^2`
`20+25=z^2`
`45=z^2`
`sqrt(3xx3xx5)=z^2`
`3sqrt5=z`
Hence the value of x, y and z are `5,2sqrt5,3sqrt5`
APPEARS IN
RELATED QUESTIONS
In below figure, If AB || CD, find the value of x.
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
State SSS similarity criterion.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
∆ABC ∼ ∆DEF, ar(∆ABC) = 9 cm2, ar(∆DEF) = 16 cm2. If BC = 2.1 cm, then the measure of EF is
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
