Advertisements
Advertisements
Question
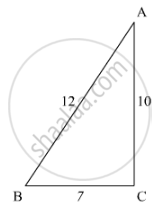
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
Solution
We have :
AD = 7.2 cm, AB = 12 cm
Therefore,
DB = 12 – 7.2 = 4.8 cm
Similarly,
AE = 6.4 cm, AC = 10 cm
Therefore,
EC = 10 – 6.4 = 3.6 cm
Now,
`(AD)/(DB)=7.2/4.8=3/2`
`(AE)/(EC)=6.4/3.6=16/9`
This,` (AD)/(DB)≠(AE)/(EC)`
Applying the converse of Thales’ theorem,
We conclude that DE is not parallel to BC.
APPEARS IN
RELATED QUESTIONS
ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
State SSS similarity criterion.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
