Advertisements
Advertisements
प्रश्न
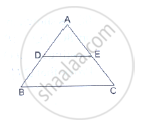
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
उत्तर
We have :
AD = 7.2 cm, AB = 12 cm
Therefore,
DB = 12 – 7.2 = 4.8 cm
Similarly,
AE = 6.4 cm, AC = 10 cm
Therefore,
EC = 10 – 6.4 = 3.6 cm
Now,
`(AD)/(DB)=7.2/4.8=3/2`
`(AE)/(EC)=6.4/3.6=16/9`
This,` (AD)/(DB)≠(AE)/(EC)`
Applying the converse of Thales’ theorem,
We conclude that DE is not parallel to BC.
APPEARS IN
संबंधित प्रश्न
In below figure, If AB || CD, find the value of x.
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
In a quadrilateral ABCD, ∠B = 90°. If AD2 = AB2 + BC2 + CD2 then prove that ∠ACD = 90°.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
