Advertisements
Advertisements
प्रश्न
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

उत्तर
GIVEN: In the given figure PQ || BC, and AP: PB = 1:2
TO FIND:\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]
We know that according to basic proportionality theorem if a line is drawn parallel to one side of a triangle intersecting the other side, then it divides the two sides in the same ratio.
Since triangle APQ and ABC are similar
Hence `(AP)/(AB)=(AQ)/(AC)=(PQ)/(BC)`
Now, it is given that `(AP)/(PB)=1/2`.
`⇒ PB =2AP`
`(AP)/(AB)=(AP)/(AP+PB)=(AP)/(AP+2AP)=1/3`
Since the ratio of the areas of two similar triangle is equal to the ratio of the squares of their corresponding sides.
Hence we got the result Area (Δ APB):Area(ΔABC)=1:9
APPEARS IN
संबंधित प्रश्न
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.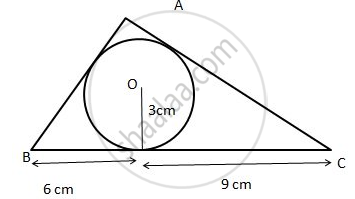
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
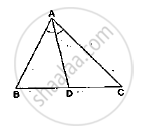
In ∆ABC, given that AB = AC and BD ⊥ AC. Prove that BC2 = 2 AC. CD
State SAS similarity criterion.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
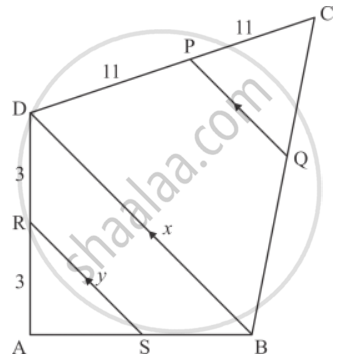
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
