Advertisements
Advertisements
प्रश्न
In the given figure, PQ || BC and AP : PB = 1 : 2. Find\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]

उत्तर
GIVEN: In the given figure PQ || BC, and AP: PB = 1:2
TO FIND:\[\frac{area \left( ∆ APQ \right)}{area \left( ∆ ABC \right)}\]
We know that according to basic proportionality theorem if a line is drawn parallel to one side of a triangle intersecting the other side, then it divides the two sides in the same ratio.
Since triangle APQ and ABC are similar
Hence `(AP)/(AB)=(AQ)/(AC)=(PQ)/(BC)`
Now, it is given that `(AP)/(PB)=1/2`.
`⇒ PB =2AP`
`(AP)/(AB)=(AP)/(AP+PB)=(AP)/(AP+2AP)=1/3`
Since the ratio of the areas of two similar triangle is equal to the ratio of the squares of their corresponding sides.
Hence we got the result Area (Δ APB):Area(ΔABC)=1:9
APPEARS IN
संबंधित प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In below Figure, ΔABC is right angled at C and DE ⊥ AB. Prove that ΔABC ~ ΔADE and Hence find the lengths of AE and DE.

In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
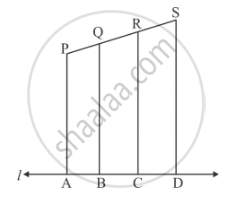
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If the median of the first triangle is 12.1 cm, then the corresponding median of the other triangle is
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
In the given figure, if ∠ADE = ∠ABC, then CE =
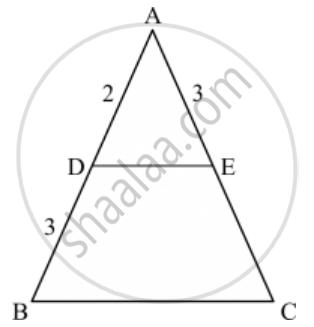
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
