Question

In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC². Prove that ΔAPC ~ ΔBCQ.

Answer 1

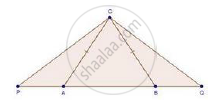
Given: In ΔABC, CA = CB and AP × BQ = AC²

To prove: ΔAPC ~ ΔBCQ

Proof:

AP × BQ = AC²                     [Given]

⇒ AP × BQ = AC × AC

⇒ AP × BQ = AC × BC               [AC = BC given]

`rArr"AP"/"BC"="AC"/"BQ"`              ......(i)

Since, CA = CB [Given]

Then, ∠CAB = ∠CBA                      …(ii) [Opposite angles to equal sides]

Now, ∠CAB + ∠CAP = 180°               …(iii) [Linear pair of angles]

And, ∠CBA + ∠CBQ = 180°          …(iv) [Linear pair of angles]

Compare equation (ii) (iii) & (iv)

∠CAP = ∠CBQ                         …(v)

In ΔAPC and ΔBCQ

∠CAP = ∠CBQ                          [From (v)]

`"AP"/"BC"="AC"/"BQ"`           [From (i)]

Then, ΔAPC~ΔBCQ                  [By SAS similarity]