Advertisements
Advertisements
प्रश्न
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

उत्तर


Let the given circle touch the sides AB and AC of the triangle at points F and E respectively and let the length of the line segment AF be x.
Now, it can be observed that:
BF = BD = 6 cm (tangents from point B)
CE = CD = 9 cm (tangents from point C)
AE = AF = x (tangents from point A)
AB = AF + FB = x + 6
BC = BD + DC = 6 + 9 = 15
CA = CE + EA = 9 + x
2s = AB + BC + CA = x + 6 + 15 + 9 + x = 30 + 2x
s = 15 + x
s – a = 15 + x – 15 = x
s – b = 15 + x – (x + 9) = 6
s – c = 15 + x – (6 + x) = 9
`"Area of " triangleABC =sqrt(s(s-a)(s-b)(s-c))`
`54=sqrt((15+x)(x)(6)(9))`
`54=3sqrt(6(15x+x^2))`
`18=sqrt(6(15x+x^2))`
`324=6(15x+x^2)`
`54=15x+x^2`
`x^2+15x-54=0`
`x^2+18x-3x-54=0`
x(x+18)-3(x+18)=0
(x+18)(x-3)=0
x = -18 and x = 3
As distance cannot be negative, x = 3
AC = 3 + 9 = 12
AB = AF + FB = 6 + x = 6 + 3 = 9
APPEARS IN
संबंधित प्रश्न
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In triangles ABC and DEF, ∠A = ∠E = 40°, AB : ED = AC : EF and ∠F = 65°, then ∠B =
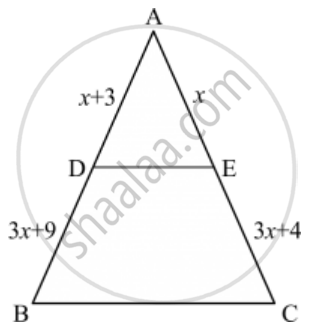
In the given figure, the value of x for which DE || AB is
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
