Advertisements
Advertisements
प्रश्न
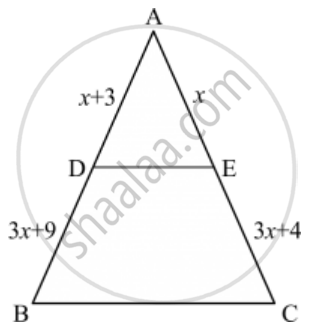
In the given figure, the value of x for which DE || AB is
विकल्प
4
1
3
2
उत्तर
Given: In ∆ABC, DE || AB.
To find: the value of x
According to basic proportionality theorem if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || AB
`(AD)/(DB)=(AE)/(EC)`
`(x+3)/(3x+19)=(x)/(3x+4)`
`(x+3)(3x+4)=(x)=(3x+19)`
`3x^2+4x+9x+12=3x^2+19x`
`19x-13x=12`
`6x=12`
`x=2`
Hence we got the result `d`.
APPEARS IN
संबंधित प्रश्न
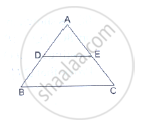
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.
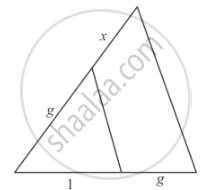
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

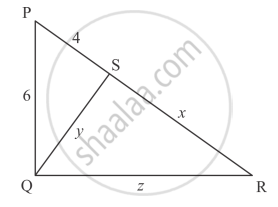
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In the adjoining figure, find AC.
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
