Advertisements
Advertisements
प्रश्न
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
विकल्प
4 : 5
5 : 4
3 : 2
5 : 7
उत्तर
Given: Two isosceles triangles have equal vertical angles and their areas are in the ratio of 16:25.
To find: Ratio of their corresponding heights.
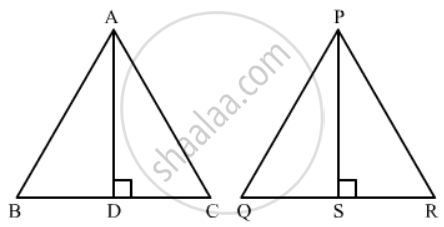
Let ∆ABC and ∆PQR be two isosceles triangles such that
\[\angle A = \angle P\]
\[ \therefore ∆ ABC~ ∆ PQR \left( SAS similarity \right)\]
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding altitudes.
Hence,
\[\frac{Ar\left( ∆ ABC \right)}{Ar\left( ∆ PQR \right)} = \left( \frac{AD}{PS} \right)^2 \]
\[ \Rightarrow \frac{16}{25} = \left( \frac{AD}{PS} \right)^2 \]
\[ \Rightarrow \frac{AD}{PS} = \frac{4}{5}\]
Hence we got the result as `a`
APPEARS IN
संबंधित प्रश्न
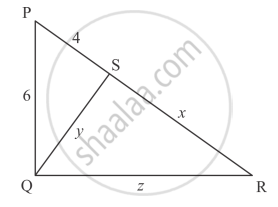
In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 4 cm, PB = 6 cm and PQ = 3 cm, determine BC.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

Corresponding sides of two triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, determine the area of the larger triangle.
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
The diagonals of quadrilateral ABCD intersect at O. Prove that
`[A(∆"ACB")]/[A(∆"ACD")] = "BO"/"DO"`
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
