Advertisements
Advertisements
प्रश्न
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
विकल्प
2 : 3
4 : 9
81 : 16
16 : 81
उत्तर
Given: Sides of two similar triangles are in the ratio 4:9
To find: Ratio of area of these triangles
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{ar(tringle 1)}/\text{ar(tringle 2)}=(\text{side1}/\text{side2})^2`
`=(4/6)^2`
`\text{ar(tringle 1)}/\text{ar(tringle 2)}=16/81`
Hence the correct answer is option `(d)`
APPEARS IN
संबंधित प्रश्न
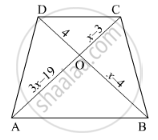
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
The area of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the smaller triangle in 3 cm, find the length of the corresponding side of the larger triangle.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
State SSS similarity criterion.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
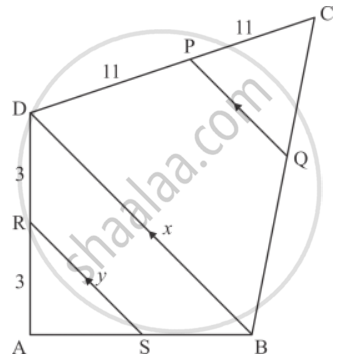
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
