Advertisements
Advertisements
प्रश्न
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is ______.
विकल्प
3 : 4
4 : 3
2 : 3
4 : 5
उत्तर
The areas of two similar triangles are in respectively 9 cm2 and 16 cm2. The ratio of their corresponding sides is 3 : 4.
Explanation:
Given: Areas of two similar triangles are 9cm2 and 16cm2.
To find: Ratio of their corresponding sides.
We know that the ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
`\text{ar(tringle 1)}/\text{ar(tringle 2)}=(\text{side1}/\text{side2})^2`
`9/16 = (\text{side1}/\text{side2})^2`
Taking square root on both sides, we get
So, the ratio of their corresponding sides is 3 : 4.
Hence the correct answer is `a`
APPEARS IN
संबंधित प्रश्न
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

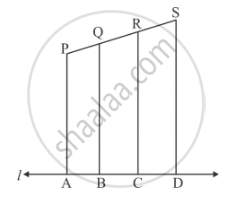
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
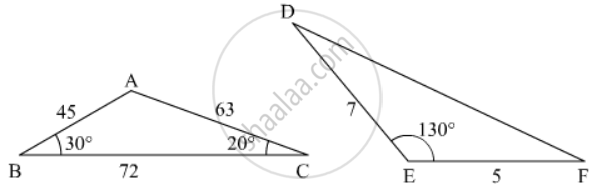
In the given figure the measure of ∠D and ∠F are respectively
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
