Advertisements
Advertisements
प्रश्न
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
उत्तर
GIVEN: AD = 2.4cm, BD = 3.6cm and AC = 5cm.
TO FIND: AE
According to BASIC PROPORTIONALITY THEOREM If a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
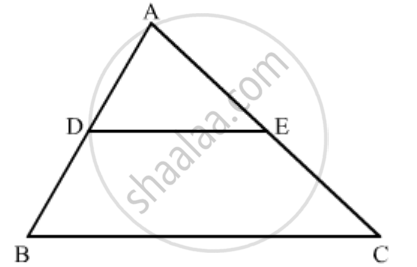
In ∆ABC, DE || BC.
`(AD)/(AB)=(AE)/(AC)`
`2.4/(2.4+3.6)=(AE)/(AC)`
`2.4/6=(AE)/(5)`
`AE=2`
`AE= 2cm`
APPEARS IN
संबंधित प्रश्न
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, the distance between their tops is
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
