Advertisements
Advertisements
प्रश्न
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
उत्तर
GIVEN: AD = 2.4cm, BD = 3.6cm and AC = 5cm.
TO FIND: AE
According to BASIC PROPORTIONALITY THEOREM If a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
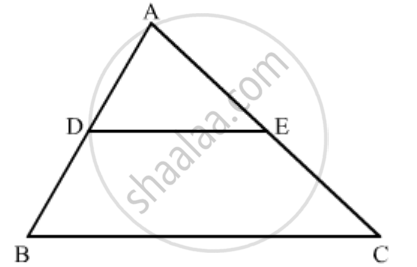
In ∆ABC, DE || BC.
`(AD)/(AB)=(AE)/(AC)`
`2.4/(2.4+3.6)=(AE)/(AC)`
`2.4/6=(AE)/(5)`
`AE=2`
`AE= 2cm`
APPEARS IN
संबंधित प्रश्न
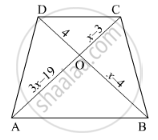
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
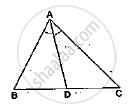
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, BD = 3.2cm and BC = 6cm, find AC.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
There is a staircase as shown in the given figure, connecting points A and B. Measurements of steps are marked in the figure. Find the straight line distance between A and B.

In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
If the areas of two similar triangles ABC and PQR are in the ratio 9 : 16 and BC = 4.5 cm, what is the length of QR?
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
