Advertisements
Advertisements
Question
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
Solution
GIVEN: AD = 2.4cm, BD = 3.6cm and AC = 5cm.
TO FIND: AE
According to BASIC PROPORTIONALITY THEOREM If a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
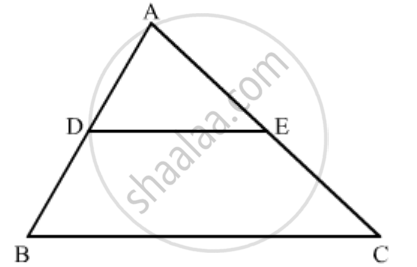
In ∆ABC, DE || BC.
`(AD)/(AB)=(AE)/(AC)`
`2.4/(2.4+3.6)=(AE)/(AC)`
`2.4/6=(AE)/(5)`
`AE=2`
`AE= 2cm`
APPEARS IN
RELATED QUESTIONS
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
What values of x will make DE || AB in the given figure?

In ∆ABC, points P and Q are on CA and CB, respectively such that CA = 16 cm, CP = 10 cm, CB = 30 cm and CQ = 25 cm. Is PQ || AB?
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
State SSS similarity criterion.
In an equilateral triangle ABC if AD ⊥ BC, then
Two isosceles triangles have equal angles and their areas are in the ratio 16 : 25. The ratio of their corresponding heights is
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
