Advertisements
Advertisements
Question
In the adjoining figure, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
Solution
GIVEN: DE is parallel to BC, AD = 1cm and BD = 2cm.
TO FIND: Ratio of ΔABC to area of ΔADE
According to BASIC PROPORTIONALITY THEOREM, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
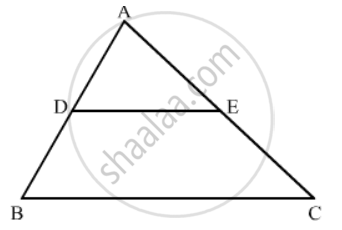
In ΔABC, DE || BC.
`(AD)/(AB)=(AE)/(AC)`
`1/(2+1)=(AE)/(AC)`
`⇒ (AE)/(AC)=1/3`
So
`(ar(Δ ABC))/(ar(Δ ADE)``=((AC)/(AE))^2`
`=(3/1)^2`
`=9/1`
APPEARS IN
RELATED QUESTIONS
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
In the given figure, l || m
(i) Name three pairs of similar triangles with proper correspondence; write similarities.
(ii) Prove that

In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[DC = \frac{ab}{b + c}\]
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
∆ABC and ∆BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangle ABC and BDE is
In ∆ABC, D and E are points on side AB and AC respectively such that DE || BC and AD : DB = 3 : 1. If EA = 3.3 cm, then AC =
ABCD is a trapezium such that BC || AD and AD = 4 cm. If the diagonals AC and BD intersect at O such that \[\frac{AO}{OC} = \frac{DO}{OB} = \frac{1}{2}\], then BC =
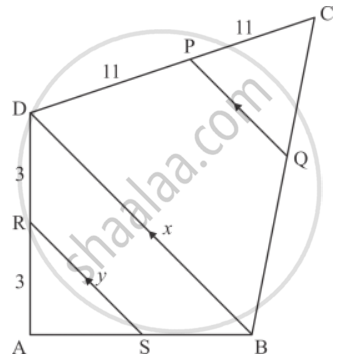
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
