Advertisements
Advertisements
Question
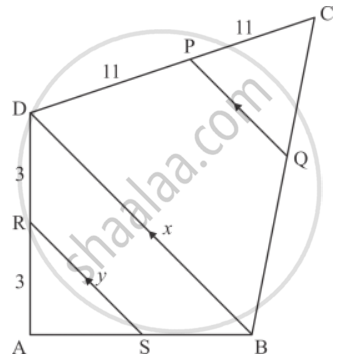
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
Options
12, 10
14, 6
10, 7
16, 8
Solution
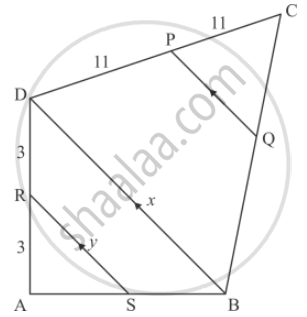
Given: RS || DB || PQ. CP = PD = 11cm and DR = RA = 3cm
To find: the value of x and y respectively.
\[In ∆ ASR and ∆ ABD, \]
\[\angle ASR = \angle ABQ \left( \text{Corresponding angles} \right)\]
\[\angle A = \angle A \left( \text{Common} \right)\]
\[ \therefore ∆ ASR ~ ∆ ABD \left( AA \hspace{0.167em} \text{Similarity} \right)\]
`(AR)/(AD)=(AS)/(AB)=(RS)/(DB)`
`3/6=(RS)/(DB)`
`1/2=x/y`
`x=2y`
This relation is satisfied by option (d).
Hence, x = 16 cm and y = 8cm
Hence the result is `d`
APPEARS IN
RELATED QUESTIONS
The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
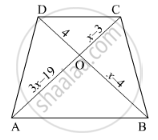
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
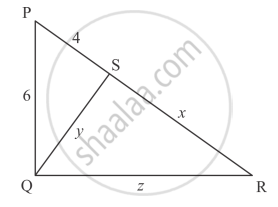
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. Find AC
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
