Advertisements
Advertisements
Question
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
Options
- \[\frac{3}{4}\]
- \[\frac{1}{3}\]
- \[\frac{1}{4}\]
- \[\frac{2}{3}\]
Solution

Given: PB||CF and DP||EF. AB = 2 cm and AC = 8 cm.
To find: AD: DE
According to BASIC PROPORTIONALITY THEOREM, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ACF, PB || CF.
`(AB)/(BC)=(AP)/(PF)`
`(AP)/(PF)=2/(8-2)`
`(AP)/(PF)=2/6`
`(AP)/(PF)=1/3........(1)`
Again, DP||EF.
`(AD)/(DE)=(AP)/(PF)`
`(AD)/(DE)=1/3`
Hence we got the result Option `b`.
APPEARS IN
RELATED QUESTIONS
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
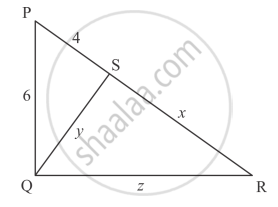
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
In ∆ABC, ray AD bisects ∠A and intersects BC in D. If BC = a, AC = b and AC = c, prove that \[BD = \frac{ac}{b + c}\]
In the adjoining figure, find AC.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then, length of DE (in cm) is ______.
