Advertisements
Advertisements
Question
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
Options
4 AC2
5 AC2
- \[\frac{5}{4} {AC}^2\]
6 AC2
Solution
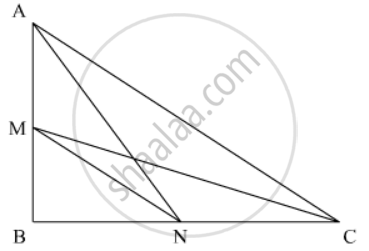
M is the mid-point of AB.
∴ \[BM = \frac{AB}{2}\]
N is the mid-point of BC.
∴\[BN = \frac{BC}{2}\]
Now,
`AN^2+CM^2=(AB^2+(BC)^2)+((AB)^2+BC^2)`
`=AB^2+BC^2+1/4AB^2+BC^2`
`=5/4(AB^2+BC^2)`
`⇒ 4(AN^2+CM^2)=5AC^2`
Hence option (b) is correct.
APPEARS IN
RELATED QUESTIONS
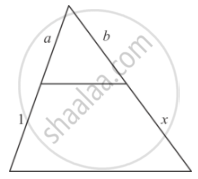
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
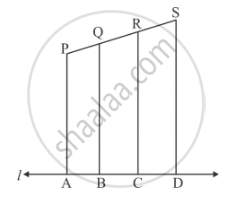
In the given figure, each of PA, QB, RC and SD is perpendicular to l. If AB = 6 cm, BC = 9 cm, CD = 12 cm and PS = 36 cm, then determine PQ, QR and RS.
In a triangle ABC, N is a point on AC such that BN ⊥ AC. If BN2 = AN . NC, prove that ∠B = 90°.
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
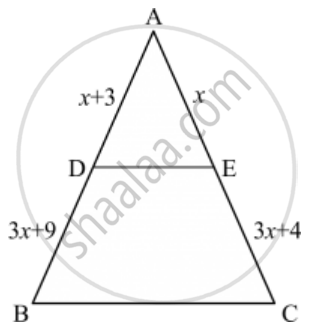
In the given figure, the value of x for which DE || AB is
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. The height of the tower is
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
