Advertisements
Advertisements
Question
If ∆ABC ∼ ∆DEF such that AB = 9.1 cm and DE = 6.5 cm. If the perimeter of ∆DEF is 25 cm, then the perimeter of ∆ABC is
Options
36 cm
30 cm
34 cm
35 cm
Solution
Given: ΔABC is similar to ΔDEF such that AB= 9.1cm, DE = 6.5cm. Perimeter of ΔDEF is 25cm.
To find: Perimeter of ΔABC.
We know that the ratio of corresponding sides of similar triangles is equal to the ratio of their perimeters.
Hence,
`(AB)/(DE)=(BC)/(EF)=(AC)/(DE)=(P1)/(P2)`
`(AB)/(DE)=(P(Δ ABC))/(P(Δ DEF))`
`9.1/6.5=(P(Δ ABC))/25`
`P(Δ ABC)=(9.1xx25)/6.5`
`P(Δ ABC)=35cm`
Hence the correct answer is `d`
APPEARS IN
RELATED QUESTIONS
In the below figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of Δ ABC is 54 cm2, then find the lengths of sides AB and AC.

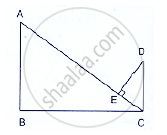
In Figure below, if AB ⊥ BC, DC ⊥ BC and DE ⊥ AC, Prove that Δ CED ~ ABC.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
State AAA similarity criterion.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
State Pythagoras theorem and its converse.
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
