Advertisements
Advertisements
Question
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
Solution

We have,
Height of girl = 90 cm = 0.9 m
Height of lamp-post = 3.6 m
Speed of girl = 1.2 m/sec
∴ Distance moved by girl (CQ) = Speed × Time
= 1.2 × 4 = 4.8m
Let length of shadow (AC) = x cm
In ΔABC and ΔAPQ
∠ACB = ∠AQP [Each 90°]
∠BAC = ∠PAQ [Common]
Then, ΔAB ~ ΔAPQ [By AA similarity]
`therefore"AC"/"AQ"="BC"/"PQ"` [Corresponding parts of similar Δ are proportional]
`rArrx/(x+4.8)=0.9/3.6`
`rArrx/(x+4.8)=1/4`
⇒ 4x = x + 4.8
⇒ 4x – x = 4.8
⇒ 3x = 4.8
`rArrx=4.8/3=1.6` m
∴ Length of shadow = 1.6m
APPEARS IN
RELATED QUESTIONS
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
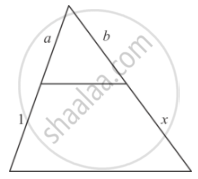
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
If ABC and DEF are similar triangles such that ∠A = 57° and ∠E = 73°, what is the measure of ∠C?
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
If ABC is a right triangle right-angled at B and M, N are the mid-points of AB and BC respectively, then 4(AN2 + CM2) =
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
