Advertisements
Advertisements
Question
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
Options
- \[\frac{BC}{DF} = \frac{AC}{DE}\]
- \[\frac{AB}{DE} = \frac{BC}{DF}\]
- \[\frac{AB}{EF} = \frac{AC}{DE}\]
- \[\frac{BC}{DF} = \frac{AB}{EF}\]
Solution
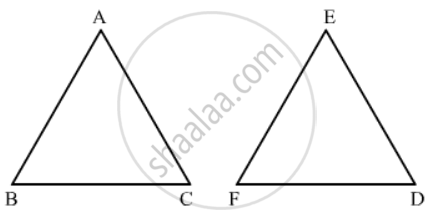
In ΔABC and ΔDEF
`∠ A = ∠ E`
`∠ B = ∠ F`
∴ ΔABC and ΔDEF are similar triangles.
Hence `(AB)/(EF)=(BC)/(FD)=(CA)/(DE)`
Hence the correct answer is (b).
APPEARS IN
RELATED QUESTIONS
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using similarity criterion for two triangles, show that `"OA"/"OC"="OB"/"OD"`.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

A ladder is placed in such a way that its foot is at a distance of 15m from a wall and its top reaches a window 20m above the ground. Find the length of the ladder.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
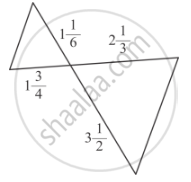
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
If ∆ABC and ∆DEF are similar such that 2AB = DE and BC = 8 cm, then EF =
If in two triangles ABC and DEF, \[\frac{AB}{DE} = \frac{BC}{FE} = \frac{CA}{FD}\], then
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
