Advertisements
Advertisements
Question
In the given figure the measure of ∠D and ∠F are respectively
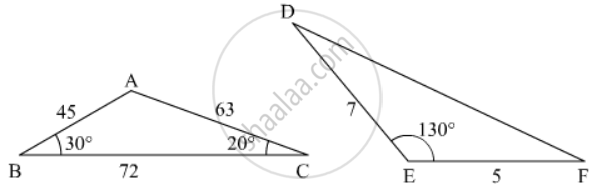
Options
50°, 40°
20°, 30°
40°, 50°
30°, 20°
Solution
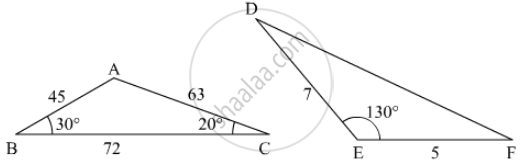
ΔABC and ΔDEF,
\[\frac{AB}{AC} = \frac{EF}{ED}\]
\[\angle A = \angle E = 130^o\]
ΔABC ∼
ΔEFD (SAS Similarity)
\[\angle D = \angle C = 20^o\]
Hence the correct answer is `b`
APPEARS IN
RELATED QUESTIONS
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In ∆PQR, M and N are points on sides PQ and PR respectively such that PM = 15 cm and NR = 8 cm. If PQ = 25 cm and PR = 20 cm state whether MN || QR.
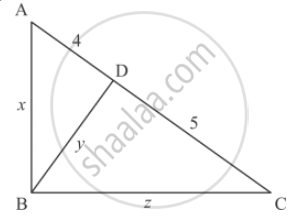
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
Prove that in an equilateral triangle, three times the square of a side is equal to four times the square of its altitudes.
In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
If ABC and DEF are similar triangles such that ∠A = 47° and ∠E = 83°, then ∠C =
If in ∆ABC and ∆DEF, \[\frac{AB}{DE} = \frac{BC}{FD}\], then ∆ABC ∼ ∆DEF when
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
