Advertisements
Advertisements
प्रश्न
In the given figure the measure of ∠D and ∠F are respectively
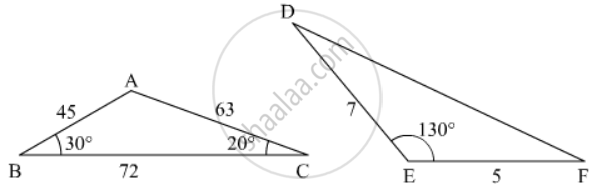
पर्याय
50°, 40°
20°, 30°
40°, 50°
30°, 20°
उत्तर
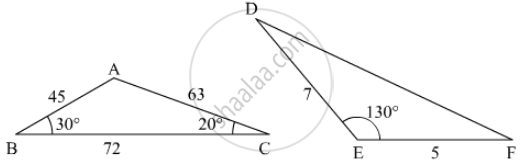
ΔABC and ΔDEF,
\[\frac{AB}{AC} = \frac{EF}{ED}\]
\[\angle A = \angle E = 130^o\]
ΔABC ∼
ΔEFD (SAS Similarity)
\[\angle D = \angle C = 20^o\]
Hence the correct answer is `b`
APPEARS IN
संबंधित प्रश्न
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
If ∆ABC and ∆DEF are similar triangles such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm and EF = 4 cm, write the perimeter of ∆DEF.
If ∆ABC is an equilateral triangle such that AD ⊥ BC, then AD2 =
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
If in two triangle ABC and DEF, ∠A = ∠E, ∠B = ∠F, then which of the following is not true?
(a)\[\frac{BC}{DF} = \frac{AC}{DE}\]
(b)\[\frac{AB}{DE} = \frac{BC}{DF}\]
(c)\[\frac{AB}{EF} = \frac{AC}{DE}\]
(d)\[\frac{BC}{DF} = \frac{AB}{EF}\]
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
