Advertisements
Advertisements
प्रश्न
A man goes 24 m due west and then 7 m due north. How far is he from the starting point?
पर्याय
31 m
17 m
25 m
26 m
उत्तर
A man goes 24m due to west and then 7m due north.
Let the man starts from point B and goes 24 m due to west and reaches point A, then walked 7m north and reaches point C.
Now we have to find the distance between the starting point and the end point i.e. BC.
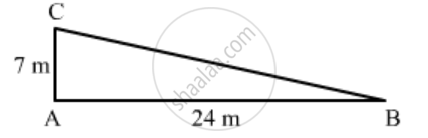
In right triangle ABC, applying Pythagoras theorem, we get
`BC^2=AB^2+AC^2`
`BC^2=(24)^2+(7)^2`
`BC^2=576+49`
`BC^2=625`
`BC=25m`
Hence correct answer is `c`.
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In the given figure, DE || BD. Determine AC and AE.

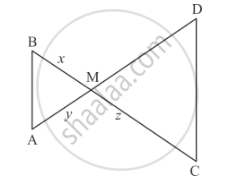
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
State Pythagoras theorem and its converse.
If D, E, F are the mid-points of sides BC, CA and AB respectively of ∆ABC, then the ratio of the areas of triangles DEF and ABC is
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 6 cm, AC = 5 cm and BD = 3 cm, then DC =
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
