Advertisements
Advertisements
प्रश्न
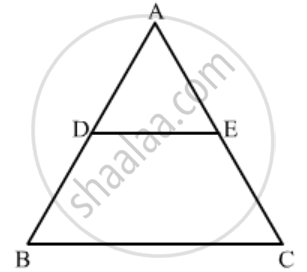
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
पर्याय
3 : 4
9 : 16
3 : 5
9 : 25
उत्तर
Given: In ΔABC, D is on side AB and point E is on side AC, such that BCED is a trapezium. DE: BC = 3:5.
To find: Calculate the ratio of the areas of ΔADE and the trapezium BCED.
In ΔADE and ΔABC,
\[\angle ADE = \angle B \left( \text{Corresponding angles} \right)\]
\[\angle A = \angle A \left( \text{Common} \right)\]
\[ \therefore ∆ ADE~ ∆ ABC \left( \text{AA Similarity} \right)\]
We know that
`(Ar(Δ ADE))/(Ar(ΔABC))=(DE)^2/(BC)^2`
`(Ar(Δ ADE))/(Ar(ΔABC))= 3^2/5^2`
`(Ar(Δ ADE))/(Ar(ΔABC))= 9/25`
Let Area of ΔADE = 9x sq. units and Area of ΔABC = 25x sq. units
`Ar [trap BCED]=Ar(Δ ABC) - Ar (Δ ADE)`
`= 25x -9x`
`16x`sq units
`Now ,`
`(Ar(Δ ADE))/(Ar(trapBCED))= (9x)/(16x)`
`(Ar(Δ ADE))/(Ar(trapBCED))= 9/16`
Hence the correct answer is `b`.
APPEARS IN
संबंधित प्रश्न
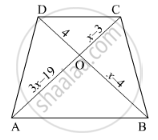
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
In an isosceles ΔABC, the base AB is produced both the ways to P and Q such that AP × BQ = AC2. Prove that ΔAPC ~ ΔBCQ.
In a ΔABC, AD is the bisector of ∠A.
If AB = 5.6cm, AC = 4cm and DC = 3cm, find BC.

In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
In a quadrilateral ABCD, given that ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2.
In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
State Pythagoras theorem and its converse.
