Advertisements
Advertisements
प्रश्न
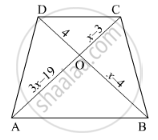
In below figure, AB || CD. If OA = 3x – 19, OB = x – 4, OC = x – 3 and OD = 4, find x.
उत्तर
Since diagonals of a trapezium divide each other proportionally.
`therefore"AO"/"OC"="BO"/"OD"`
`rArr(3x-19)/(x-3)=(x-4)/4`
⇒ 4(3𝑥 − 19) = (𝑥 − 4)(𝑥 − 3)
⇒ 12x – 76 = x (x – 3) −4(x – 3)
⇒ 12𝑥 − 76 = 𝑥2 − 3𝑥 − 4𝑥 + 12
⇒ 𝑥2 − 7𝑥 − 12𝑥 + 12 + 76 = 0
⇒ 𝑥2 − 19𝑥 + 88 = 0
⇒ 𝑥2 − 11x − 8x + 88 = 0
⇒ 𝑥(𝑥 − 11) − 8(𝑥 − 11) = 0
⇒ (𝑥 − 11)(𝑥 − 8) = 0
⇒ 𝑥 − 11 = 0 or x – 8 = 0
⇒ x = 11 or x = 8
APPEARS IN
संबंधित प्रश्न
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
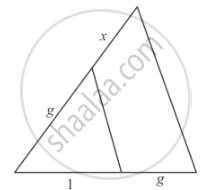
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :
In each of the following figures, you find who triangles. Indicate whether the triangles are similar. Give reasons in support of your answer.

ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
Corresponding sides of two similar triangles are in the ratio 1 : 3. If the area of the smaller triangle in 40 cm2, find the area of the larger triangle.
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

In the figure given below DE || BC. If AD = 2.4 cm, DB = 3.6 cm, AC = 5 cm. Find AE.
In the given figure, ∆AHK is similar to ∆ABC. If AK = 10 cm, BC = 3.5 cm and HK = 7 cm, find AC.

If ∆ABC and ∆DEF are two triangles such tha\[\frac{AB}{DE} = \frac{BC}{EF} = \frac{CA}{FD} = \frac{2}{5}\] , then Area (∆ABC) : Area (∆DEF) =
