Advertisements
Advertisements
प्रश्न
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.

उत्तर
Let us take
AB = Tip of fishing rod above the surface of the water
BC = The string rest from directly under the tip of the rod.
AC = The length of string

In ABC right triangle right angled at B
`AC^2=AB^2+BC^2`
`AC^2=1.8^2+2.4^2`
`AC^2=3.24+5.76`
`AC^2=9`
`AC^2=sqrt9`
`AC^2sqrt(3xx3)`
Hence 3 m string is out
The string pulled in 12 seconds is equal to `12xx5=60cm=0.6m` to point D
In this case the diagram will look like the following

Now The length of the new string AD = AC − CD = 3.00 − 0.6 = 2.4 m
Now in triangle ADB we have
`1.8^2+BD^2=2.4^2`
`3.24+BD^2=5.76`
`BD^2=5.76-3.24`
`BD^2=2.52`
`BD=1.587`
∴ Required distance = `1.587+1.2=2.79 m`
Hence, the horizontal distance is `2.97m.`
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
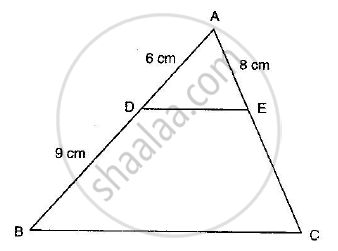
In each of the figures [(i)-(iv)] given below, a line segment is drawn parallel to one side of the triangle and the lengths of certain line-segment are marked. Find the value of x in each of the following :

ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
In the adjoining figure, find AC.
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
In a ∆ABC, ∠A = 90°, AB = 5 cm and AC = 12 cm. If AD ⊥ BC, then AD =
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
∆ABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ∆DEF ∼ ∆ABC and EF = 4 cm, then perimeter of ∆DEF is
In ∆ABC, a line XY parallel to BC cuts AB at X and AC at Y. If BY bisects ∠XYC, then
