Advertisements
Advertisements
प्रश्न
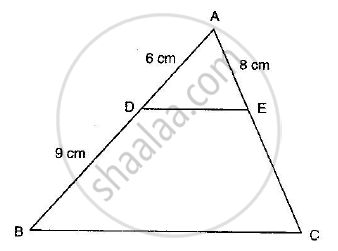
In the adjoining figure, find AC.
उत्तर
GIVEN: In the figure we are given AD = 6cm, BD = 9cm, AE = 8cm
TO FIND: AC
According to BASIC PROPORTIONALITY THEOREM, if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || BC. So,
`(AD)/(DB)=(AE)/(EC)`
`6/9=8/(EC)`
`EC=(8xx9)/6`
`EC=12cm`
Now,
`AC=AE+EC`
`AC=8+12`
`AC=20cm`
APPEARS IN
संबंधित प्रश्न
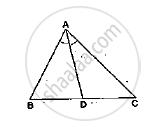
In a ΔABC, AD is the bisector of ∠A.
If AB = 6.4cm, AC = 8cm and BD = 5.6cm, find DC.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
In the given figure,

AB || DC prove that
DM × BV = BM ✕ DU
ABCD is a trapezium having AB || DC. Prove that O, the point of intersection of diagonals, divides the two diagonals in the same ratio. Also prove that
In ∆ABC, AD is a median. Prove that AB2 + AC2 = 2AD2 + 2DC2.
The areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26 cm, what is the length of the longest side of the smaller triangle?
In the given figure, LM = LN = 46°. Express x in terms of a, b and c where a, b, c are lengths of LM, MN and NK respectively.

XY is drawn parallel to the base BC of a ∆ABC cutting AB at X and AC at Y. If AB = 4 BX and YC = 2 cm, then AY =
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
In the given figure, if PB || CF and DP || EF, then \[\frac{AD}{DE} =\]
