Advertisements
Advertisements
प्रश्न
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
उत्तर
In Δ ABC, P and Q are points on sides AB and AC respectively such that `PQ|| BC`
Then we have
`(AP)/(AB)=(AQ)/(AC)`
AP = 3cm ,PB = 5cm ,AC = 8cm and AB = cm
`3/8=(AQ)/8`
`3/cancel8=(AQ)/cancel8`
`3= AQ`
Hence the value of AQ is 3 cm.
APPEARS IN
संबंधित प्रश्न
the below given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC are respectively of lengths 6 cm and 9 cm. If the area of ΔABC is 54 cm2, then find the lengths of sides AB and AC.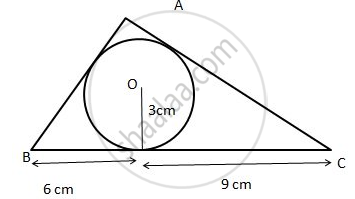
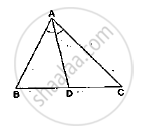
In a ΔABC, AD is the bisector of ∠A.
If AB = 10cm, AC = 14cm and BC = 6cm, find BD and DC.
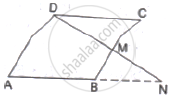
M is a point on the side BC of a parallelogram ABCD. DM when produced meets AB produced at N. Prove that
(1)` (DM)/(MN)=(DC)/(BN)`
(2)` (DN)/(DM)=(AN)/(DC)`
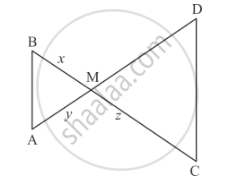
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
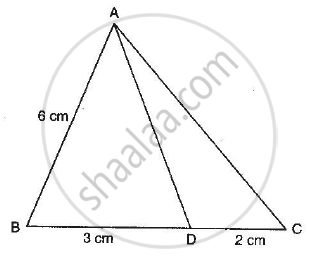
In the adjoining figure, if AD is the bisector of ∠A, what is AC?
If the altitude of two similar triangles are in the ratio 2 : 3, what is the ratio of their areas?
The lengths of the diagonals of a rhombus are 30 cm and 40 cm. Find the side of the rhombus.
The length of the hypotenuse of an isosceles right triangle whose one side is\[4\sqrt{2} cm\]
∆ABC is an isosceles triangle in which ∠C = 90. If AC = 6 cm, then AB =
