Advertisements
Advertisements
प्रश्न
In ∆ABC, ∠C is an obtuse angle. AD ⊥ BC and AB2 = AC2 + 3 BC2. Prove that BC = CD.
उत्तर
Given: ΔABC where ∠C is an obtuse angle, AD ⊥ BC and AB2 = AC2 + 3BC2

To prove: BC = CD
Proof:
In ΔABC, ∠C is obtuse.
Therefore,
AB2 = AC2 + BC2 + 2BC × DC (Obtuse angle theorem) …(1)
AB2 = AC2 + 3BC2 (Given) …(2)
From (1) and (2), we get
AC2 + 3BC2 = AC2 + BC2 + 2BC × DC
⇒ 3BC2 = BC2 + 2BC × DC
⇒ 2BC2 = 2BC × DC
⇒ BC = DC
APPEARS IN
संबंधित प्रश्न
In ∆ABC, the bisector of ∠A intersects BC in D. If AB = 18 cm, AC = 15 cm and BC = 22 cm, find BD.
In the given figure,

AB || DC prove that
(i) ∆DMU ∼ ∆BMV
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
In each of the figures given below, an altitude is drawn to the hypotenuse by a right-angled triangle. The length of different line-segment are marked in each figure. Determine x, y, z in each case.
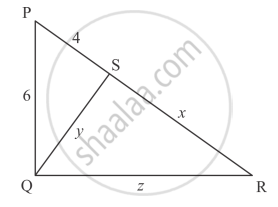
In ∆ABC, if BD ⊥ AC and BC2 = 2 AC . CD, then prove that AB = AC.
The areas of two similar triangles ∆ABC and ∆DEF are 144 cm2 and 81 cm2 respectively. If the longest side of larger ∆ABC be 36 cm, then the longest side of the smaller triangle ∆DEF is
∆ABC ∼ ∆PQR such that ar(∆ABC) = 4 ar(∆PQR). If BC = 12 cm, then QR =
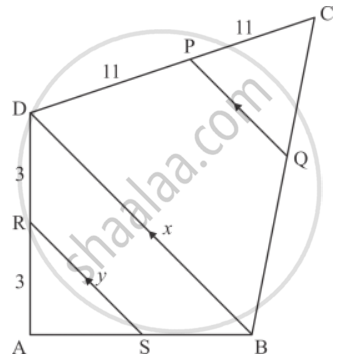
In the given figure, RS || DB || PQ. If CP = PD = 11 cm and DR = RA = 3 cm. Then the values of x and y are respectively.
A chord of a circle of radius 10 cm subtends a right angle at the centre. The length of the chord (in cm) is
If ABC is an isosceles triangle and D is a point of BC such that AD ⊥ BC, then
