Advertisements
Advertisements
प्रश्न
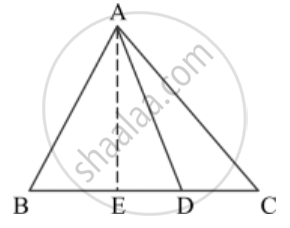
A point D is on the side BC of an equilateral triangle ABC such that\[DC = \frac{1}{4}BC\]. Prove that AD2 = 13 CD2.
उत्तर
We are given ABC is an equilateral triangle with `CD = 1/2 BC`
We have to prove `AD^2 = 13DC^2`
Draw `AE ⊥ BC`
In Δ AEB and ΔAED we have `AB =AC`
`∠ AEB = ∠ AEC = 90^o `
`AE = AE`
So by right side criterion of similarity we have
Thus we have
`DC =1/4BC and BE =EC = 1/2 BC`
Since `∠ C= 60^o` therefore
`AD^2 =AC^2+DC^2 - 2DC xxEC`
`AD^2 = AC^2(1/4BC)^2-2xx1/4BCxx1/2BC`
`AS^2=AC^2+1/16BC^2-2xx1/2BCxx1/2BC`
`AD^2=AC^2+1/16BC^2-BC^2`
We know that AB = BC = AC
`AD^2=BC^2+1/16BC^2-BC^2`
`AD^2=(16BC^2+1BC^2-4BC^2)/16`
`AD^2=13/16BC^2`
We know that `DC = 1/4 BC`
`4DC=BC`
Substitute `4DC=BC` in `AD^2 =13/16BC^2 ` we get
`AD^2 = 13/16xx(4DC)^2`
`AD^2 = 13/16xx16DC^2`
`AD^2 = 13/16xx16xxDC^2`
`AD^2=13DC^2`
Hence we have proved that `AD^2 = 13 DC^2`
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AD = 5.7cm, DB = 9.5cm, AE = 4.8cm and EC = 8cm.

D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
A 13m long ladder reaches a window of a building 12m above the ground. Determine the distance of the foot of the ladder from the building.
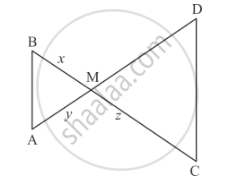
In the given figure, ∆AMB ∼ ∆CMD; determine MD in terms of x, y and z.
In ∆ABC, D and E are points on sides AB and AC respectively such that AD ✕ EC = AE ✕ DB. Prove that DE || BC.
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

∆ABC ∼ ∆DEF. If BC = 3 cm, EF = 4 cm and ar(∆ABC) = 54 cm2, then ar(∆DEF) =
In a ∆ABC, perpendicular AD from A and BC meets BC at D. If BD = 8 cm, DC = 2 cm and AD = 4 cm, then
∆ABC is such that AB = 3cm, BC = 2cm, CA = 2.5cm. If ∆ABC ~ ∆DEF and EF = 4cm, then perimeter of ∆DEF is ______.
