Advertisements
Advertisements
प्रश्न
ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN ⊥ BD. Prove that BM2 + BN2 = DM2 + DN2.
उत्तर
Given: A rectangle ABCD where AM ⊥ BD and CN ⊥ BD.
To prove: BM2 + BN2 = DM2 + DN2
Proof:
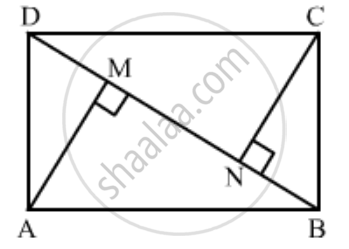
Apply Pythagoras Theorem in ΔAMB and ΔCND,
AB2 = AM2 + MB2
CD2 = CN2 + ND2
Since AB = CD, AM2 + MB2 = CN2 + ND2
⇒ AM2 − CN2 = ND2 − MB2 … (i)
Again apply Pythagoras Theorem in ΔAMD and ΔCNB,
AD2 = AM2 + MD2
CB2 = CN2 + NB2
Since AD = BC, AM2 + MD2 = CN2 + NB2
⇒ AM2 − CN2 = NB2 − MD2 … (ii)
Equating (i) and (ii),
ND2 − MB2 = NB2 − MD2
I.e., BM2 + BN2 = DM2 + DN2
This proves the given relation.
APPEARS IN
संबंधित प्रश्न
D and E are points on the sides AB and AC respectively of a ΔABC. In each of the following cases, determine whether DE║BC or not.
AB = 11.7cm, AC = 11.2cm, BD = 6.5cm and AE = 4.2cm.
In ∆ABC, P and Q are points on sides AB and AC respectively such that PQ || BC. If AP = 3 cm, PB = 5 cm and AC = 8 cm, find AQ.
ABCD is a trapezium in which AB || DC. P and Q are points on sides AD and BC such that PQ || AB. If PD = 18, BQ = 35 and QC = 15, find AD.
In ∆ABC, AD and BE are altitude. Prove that\[\frac{ar\left( ∆ DEC \right)}{ar\left( ∆ ABC \right)} = \frac{{DC}^2}{{AC}^2}\]
In the given figure, DE || BC in ∆ABC such that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.

Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio.
In an equilateral triangle ABC if AD ⊥ BC, then AD2 =
In a ∆ABC, point D is on side AB and point E is on side AC, such that BCED is a trapezium. If DE : BC = 3 : 5, then Area (∆ ADE) : Area (◻BCED) =
∆ABC is a right triangle right-angled at A and AD ⊥ BC. Then, \[\frac{BD}{DC} =\]
In an isosceles triangle ABC if AC = BC and AB2 = 2AC2, then ∠C =
