Question

ABCD is a rectangle. Points M and N are on BD such that AM ⊥ BD and CN  ⊥ BD. Prove that BM² + BN² = DM² + DN².

Answer 1

Given: A rectangle ABCD where AM ⊥ BD and CN ⊥ BD.

To prove: BM² + BN² = DM² + DN²

Proof:

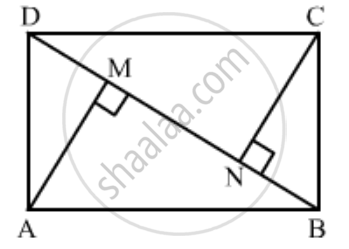
Apply Pythagoras Theorem in ΔAMB and ΔCND,

AB² = AM² + MB²

CD² = CN² + ND²

Since AB = CD, AM² + MB² = CN² + ND²

⇒ AM² − CN² = ND² − MB² … (i)

Again apply Pythagoras Theorem in ΔAMD and ΔCNB,

AD² = AM² + MD²

CB² = CN² + NB²

Since AD = BC, AM² + MD² = CN² + NB²

⇒ AM² − CN² = NB² − MD² … (ii)

Equating (i) and (ii),

ND² − MB² = NB² − MD²

I.e., BM² + BN² = DM² + DN²

This proves the given relation.