Question

ABCD is a quadrilateral in which AD = BC. If P, Q, R, S be the mid-points of AB, AC, CD and BD respectively, show that PQRS is a rhombus.

Answer 1

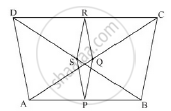
AD = BC and P, Q, R and S are the mid-points of sides AB, AC, CD and BD respectively, show that PQRS is a rhombus.

In ΔBAD, by mid-point theorem

PS || AD and PS `=1/2` AD              .......(i)

In ΔCAD, by mid-point theorem

QR || AD and QR `=1/2` AD              .......(ii)

Compare (i) and (ii)

PS || QR and PS = QR

Since one pair of opposite sides is equal as well as parallel then

PQRS is a parallelogram                     ...(iii)

Now, In ΔABC, by mid-point theorem

PQ || BC and PQ `=1/2` BC                .......(iv)

And, AD = BC                                …(v) [given]

Compare equations (i) (iv) and (v)

PS = PQ …(vi)

From (iii) and (vi)

Since, PQRS is a parallelogram with PS = PQ then PQRS is a rhombus.