Advertisements
Advertisements
प्रश्न
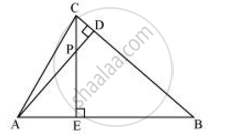
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
उत्तर
We have,
AL ⊥ BC and CM ⊥ AB
In Δ OMA and ΔOLC
∠MOA = ∠LOC [Vertically opposite angles]
∠AMO = ∠CLO [Each 90°]
Then, ΔOMA ~ ΔOLC [By AA similarity]
`therefore"OA"/"OC"="OM"/"OL"` [Corresponding parts of similar Δ are proportional]
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
ΔAEP ∼ ΔCDP
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
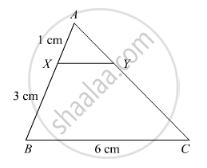
In the following figure, XY || BC. Find the length of XY.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.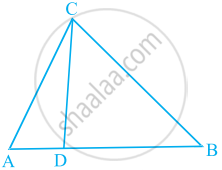
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
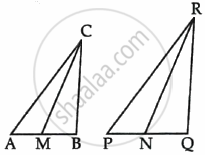
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ∼ ΔPQR, then prove that ΔAMC ∼ ΔPNR.