Advertisements
Advertisements
प्रश्न
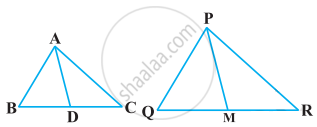
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
उत्तर
Given that,
`("AB")/("PQ") = ("AC")/("PR") = ("AD")/("PM")`
Let us extend AD and PM up to point E and L respectively, such that AD = DE and PM = ML. Then, join B to E, C to E, Q to L, and R to L.
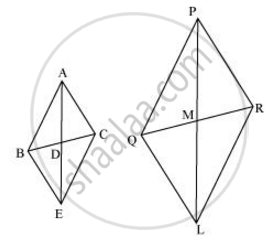
We know that medians divide opposite sides.
Therefore, BD = DC and QM = MR
Also, AD = DE ...(By construction)
And, PM = ML ...(By construction)
In quadrilateral ABEC, diagonals AE and BC bisect each other at point D.
Therefore, quadrilateral ABEC is a parallelogram.
∴ AC = BE and AB = EC ...(Opposite sides of a parallelogram are equal)
Similarly, we can prove that quadrilateral PQLR is a parallelogram and PR = QL, PQ = LR
It was given that
`("AB")/("PQ") = ("AC")/("PR") = ("AD")/("PM")`
`=>("AB")/("PQ")=("BE")/("QL")= (2"AD")/(2"PM")`
`=>("AB")/("PQ") = ("BE")/("QL") = ("AE")/("PL")`
∴ ΔABE ∼ ΔPQL ...(By SSS similarity criterion)
We know that corresponding angles of similar triangles are equal.
∴ ∠BAE = ∠QPL ...(1)
Similarly, it can be proved that ΔAEC ∼ ΔPLR and
∠CAE = ∠RPL ...(2)
Adding equation (1) and (2), we obtain
∠BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ ...(3)
In ΔABC and ΔPQR,
`("AB")/("PQ")=("AC")/("PR")`
∠CAB = ∠RPQ ...[Using equation (3)]
∴ ΔABC ∼ ΔPQR ...(By SAS similarity criterion)
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:

In the following figure, `("QR")/("QS") = ("QT")/("PR")` and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.

In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ∼ ΔECF.
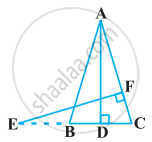
In the following figure, AB || QR. Find the length of PB.

The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
In the given figure MN|| BC and AM: MB= 1: 2
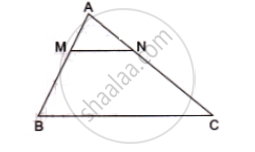
find ` (area(ΔAMN))/(area(ΔABC))`
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3 m, find how far she is away from the base of the pole.
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
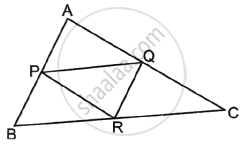
In the figure with ΔABC, P, Q, R are the mid-points of AB, AC and BC respectively. Then prove that the four triangles formed are congruent to each other.
A tangent ADB is drawn to a circle at D whose centre is C. Also, PQ is a chord parallel to AB and ∠QDB = 50°. Find the value of ∠PDQ.

In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

ABCD is a trapezium with AD ∥ BC and AD = 4 cm. If the diagonals AC and BD intersect each other at O such that AO/OC = DO/OB = 1/2, then BC = ______.
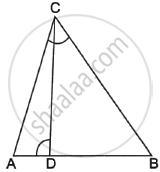
In the given figure, ∠ADC = ∠BCA; prove that ΔACB ∼ ΔADC. Hence find BD if AC = 8 cm and AD = 3 cm.
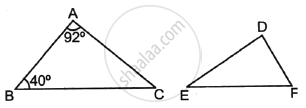
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.