Advertisements
Advertisements
प्रश्न
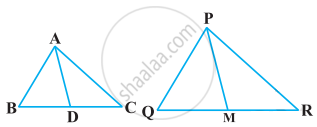
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.
उत्तर
We have MBC and PQR in which AD and PM are medians corresponding to sides BC and QR respectively such that
`("AB")/("PQ") = ("BC")/("QR") = ("AD")/("PM")`
`("AB")/("PQ") = (1/2 "BC")/(1/2 "QR") = ("AD")/("PM")`
`("AB")/("PQ") = ("BD")/("QM") = ("AD")/("PM")`
Using SSS similarity, we have
ΔABD ~ ΔPQM
Their corresponding angles are equal.
∠ABD = ∠PQM
∠ABC = ∠PQR
Now, in MBC and ΔPQR,
`("AB")/("PQ") = ("BC")/("QR")` ...[1]
Also, ∠ABC = ∠PQR ...[2]
From [1] and [2]
ΔABC ~ ΔPQR ...[SAS similarity]
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
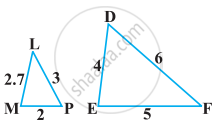
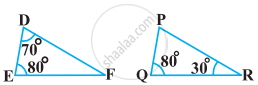
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ∼ ΔCFB.
In the following figure, AB || QR. Find the length of PB.

In the following Figure, DE || BC such that AE = (1/4) AC. If AB = 6 cm, find AD.
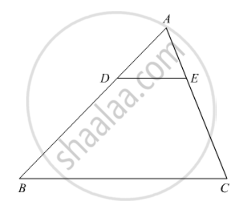
D is the mid-point of side BC of a ΔABC. AD is bisected at the point E and BE produced cuts AC at the point X. Prove that BE : EX = 3 : 1
In ΔABC, AL and CM are the perpendiculars from the vertices A and C to BC and AB respectively. If AL and CM intersect at O, prove that:
(i) ΔOMA and ΔOLC
(ii) `"OA"/"OC"="OM"/"OL"`
In the given figure, seg AC and seg BD intersect each other in point P and `"AP"/"CP" = "BP"/"DP"`. Prove that, ∆ABP ~ ∆CDP.

In ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to ______.
It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
In triangle PQR and MST, ∠P = 55°, ∠Q = 25°, ∠M = 100° and ∠S = 25°. Is ∆QPR ~ ∆TSM? Why?
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
In figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to ______.
It is given that ΔABC ~ ΔDFE, ∠A =30°, ∠C = 50°, AB = 5 cm, AC = 8 cm and DF = 7.5 cm. Then, the following is true ______.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
□ABCD is a parallelogram. Point P is the midpoint of side CD. seg BP intersects diagonal AC at point X, then prove that: 3AX = 2AC
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
