Advertisements
Advertisements
प्रश्न
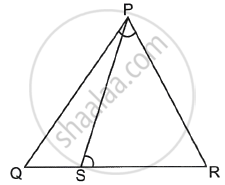
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
उत्तर
According to the question,
ΔNSQ ≅ ΔMTR
∠1 = ∠2
Since,
∆NSQ = ∆MTR
So,
SQ = TR ...(i)
Also,
∠1 = ∠2 ⇒ PT = PS ...(ii) [Since, sides opposite to equal angles are also equal]
From equations (i) and (ii),
`("PS")/("SQ") = ("PT")/("TR")`
⇒ ST || QR
By converse of basic proportionality theorem, If a line is drawn parallel to one side of a triangle to intersect the other sides in distinct points, the other two sides are divided in the same ratio.
∴ ∠1 = PQR
And
∠2 = ∠PRQ
In ∆PTS and ∆PRQ,
∠P = ∠P ...[Common angles]
∠1 = ∠PQR ...(Proved)
∠2 = ∠PRQ ...(Proved)
∴ ∆PTS – ∆PRQ ...[By AAA similarity criteria]
Hence proved.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
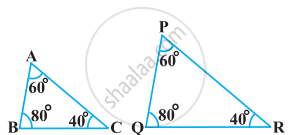
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
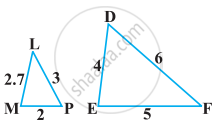
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
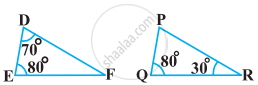
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
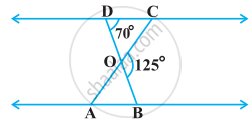
In the following figure, if ΔABE ≅ ΔACD, show that ΔADE ∼ ΔABC.
In the following Figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, find CD.

In a triangle PQR, N is a point on PR such that QN ⊥ PR. If PN . NR = QN2, prove that ∠PQR = 90°.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In the given figure, S is a point on side QR of ΔPQR such that ∠QPR = ∠PSR. Use this information to prove that PR2 = QR × SR.
In ΔABC, AP ⊥ BC, BQ ⊥ AC. If AP = 7, BQ = 8 and BC = 12, then find AC.

