Advertisements
Advertisements
प्रश्न
In figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
उत्तर
According to the question,
ΔNSQ ≅ ΔMTR
∠1 = ∠2
Since,
∆NSQ = ∆MTR
So,
SQ = TR ...(i)
Also,
∠1 = ∠2 ⇒ PT = PS ...(ii) [Since, sides opposite to equal angles are also equal]
From equations (i) and (ii),
`("PS")/("SQ") = ("PT")/("TR")`
⇒ ST || QR
By converse of basic proportionality theorem, If a line is drawn parallel to one side of a triangle to intersect the other sides in distinct points, the other two sides are divided in the same ratio.
∴ ∠1 = PQR
And
∠2 = ∠PRQ
In ∆PTS and ∆PRQ,
∠P = ∠P ...[Common angles]
∠1 = ∠PQR ...(Proved)
∠2 = ∠PRQ ...(Proved)
∴ ∆PTS – ∆PRQ ...[By AAA similarity criteria]
Hence proved.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the following figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
The sides of certain triangles are given below. Determine which of them right triangles are.
9cm, 16cm, 18cm
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
The corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
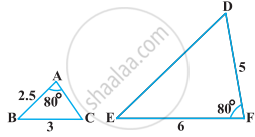
It is given that ∆ABC ~ ∆EDF such that AB = 5 cm, AC = 7 cm, DF = 15 cm and DE = 12 cm. Find the lengths of the remaining sides of the triangles.
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?
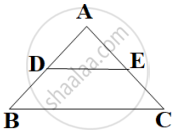
In the given figure below, `(AD)/(AE) = (AC)/(BD)` and ∠1 = ∠2, Show that ΔBAE ∼ ΔCAD.

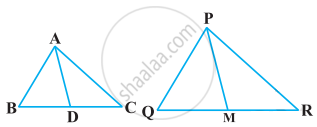
Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR show that ΔABC ~ ΔPQR.