Advertisements
Advertisements
प्रश्न
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
उत्तर
Given l || m and line segments AB, CD and EF are concurrent at point P.
To prove: `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
Proof: In ΔAPC and ΔBPD,
∠APC = ∠BPD ...[Vertically opposite angles]
∠PAC = ∠PBD ...[Alternative angles]
∴ ΔAPC ∼ ΔBPD ...[By AA similarity criterion]
Then, `("AP")/("PB") = ("AC")/("BD") = ("PC")/("PD")` ...(i)
In ΔAPE and ΔBPF,
∠APE = ∠BPF ...[Vertically opposite angles]
∠PAE = ∠PBF ...[Alternative angles]
∴ ΔAPE ∼ ΔBPF ...[By AA similarity criterion]
Then, `("AP")/("PB") = ("AE")/("BF") = ("PE")/("PF")` ...(ii)
In ΔPEC and ΔPFD,
∠EPC = ∠FPD ...[Vertically opposite angles]
∠PCE = ∠PDF ...[Alternative angles]
∴ ΔPEC ∼ ΔPFD ...[By AA similarity criterion]
Then, `("PE")/("PF") = ("PC")/("PD") = ("EC")/("FD")` ...(iii)
From equations (i), (ii) and (iii),
`("AP")/("PB") = ("AC")/("BD") = ("AE")/("BF") = ("PE")/("PF") = ("EC")/("FD")`
∴ `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
Hence proved.
APPEARS IN
संबंधित प्रश्न
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
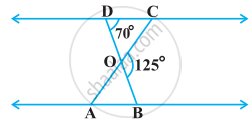
In the following figure, ΔODC ∼ ΔOBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
CD and GH are, respectively, the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG, respectively. If ΔABC ~ ΔFEG, Show that
- `("CD")/("GH") = ("AC")/("FG")`
- ΔDCB ~ ΔHGE
- ΔDCA ~ ΔHGF
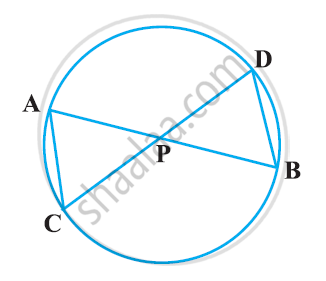
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
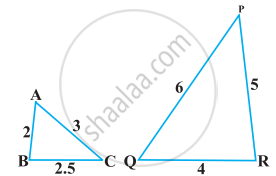
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
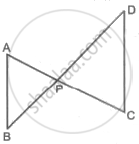
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
In the given figure, ΔLMN is similar to ΔPQR. To find the measure of ∠N, complete the following activity.
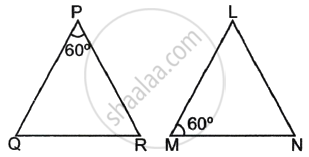
Given: ΔLMN ∼ ΔPQR
Since ΔLMN ∼ ΔPQR, therefore, corresponding angles are equal.
So, ∠L ≅ `square`
⇒ ∠L = `square`
We know, the sum of angles of a triangle = `square`
∴ ∠L + ∠M + ∠N = `square`
Substituting the values of ∠L and ∠M in equation (i),
`square` + `square` + ∠N = `square`
∠N + `square` = `square`
∠N = `square` – `square`
∠N = `square`
Hence, the measure of ∠N is `square`.
In the given figure, DE ∥ BC, AE = a units, EC = b units, DE = x units and BC = y units. Which of the following is true?