Advertisements
Advertisements
प्रश्न
In figure, l || m and line segments AB, CD and EF are concurrent at point P. Prove that `(AE)/(BF) = (AC)/(BD) = (CE)/(FD)`.
उत्तर
Given l || m and line segments AB, CD and EF are concurrent at point P.
To prove: `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
Proof: In ΔAPC and ΔBPD,
∠APC = ∠BPD ...[Vertically opposite angles]
∠PAC = ∠PBD ...[Alternative angles]
∴ ΔAPC ∼ ΔBPD ...[By AA similarity criterion]
Then, `("AP")/("PB") = ("AC")/("BD") = ("PC")/("PD")` ...(i)
In ΔAPE and ΔBPF,
∠APE = ∠BPF ...[Vertically opposite angles]
∠PAE = ∠PBF ...[Alternative angles]
∴ ΔAPE ∼ ΔBPF ...[By AA similarity criterion]
Then, `("AP")/("PB") = ("AE")/("BF") = ("PE")/("PF")` ...(ii)
In ΔPEC and ΔPFD,
∠EPC = ∠FPD ...[Vertically opposite angles]
∠PCE = ∠PDF ...[Alternative angles]
∴ ΔPEC ∼ ΔPFD ...[By AA similarity criterion]
Then, `("PE")/("PF") = ("PC")/("PD") = ("EC")/("FD")` ...(iii)
From equations (i), (ii) and (iii),
`("AP")/("PB") = ("AC")/("BD") = ("AE")/("BF") = ("PE")/("PF") = ("EC")/("FD")`
∴ `("AE")/("BF") = ("AC")/("BD") = ("CE")/("FD")`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the following figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:

ΔPDC ∼ ΔBEC
The sides of certain triangles are given below. Determine which of them right triangles are.
(a – 1) cm, `2sqrta` cm, (a + 1) cm
Two triangles DEF an GHK are such that ∠D = 48° and ∠H = 57° . If ΔDEF ∼GHK then find the measures of ∠F
In figure, if AB || DC and AC and PQ intersect each other at the point O, prove that OA . CQ = OC . AP
In the figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.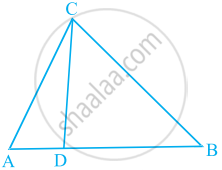
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.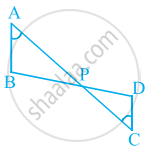
If in two triangles ABC and PQR, `(AB)/(QR) = (BC)/(PR) = (CA)/(PQ)`, then ______.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are ______.
If in triangles ABC and DEF, `(AB)/(DE) = (BC)/(FD)`, then they will be similar, when ______.
Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles POQ and ROS.
