Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
उत्तर
Given: Quadrilateral ABCD, in which ∠A + ∠D = 90°
To prove: AC2 + BD2 = AD2 + BC2
Construct: Produce AB and CD to meet at E
Also join AC and BD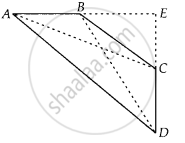
Proof: In ∆AED, ∠A + ∠D = 90° ...[Given]
∴ ∠E = 180° – (∠A + ∠D) = 90° ...[∵ Sum of angles of a triangle = 180°]
Then, by Pythagoras theorem,
AD2 = AE2 + DE2
In ∆BEC, by Pythagoras theorem,
BC2 = BE2 + EC2
On adding both equations, we get
AD2 + BC2 = AE2 + DE2 + BE2 + CE2 ...(i)
In ∆AEC, by Pythagoras theorem,
AC2 = AE2 + CE2
And in ∆BED, by Pythagoras theorem,
BD2 = BE2 + DE2
On adding both equations, we get
AC2 + BD2 = AE2 + CE2 + BE2 + DE2 ...(ii)
From equations (i) and (ii),
AC2 + BD2 = AD2 + BC2
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
In equilateral Δ ABC, AD ⊥ BC and BC = x cm. Find, in terms of x, the length of AD.
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
In the adjoining figure, a tangent is drawn to a circle of radius 4 cm and centre C, at the point S. Find the length of the tangent ST, if CT = 10 cm.

Two circles having same circumference are congruent.
