Advertisements
Advertisements
प्रश्न
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
उत्तर
Given: In ∆PQR,
PD ⊥ QR,
PQ = a,
PR = b,
QD = c
And DR = d
To prove: (a + b)(a – b) = (c + d)(c – d)
Proof: In right angled ΔPDQ,
PQ2 = PD2 + QD2 ...[By pythagoras theorem]
⇒ a2 = PD2 + c2
⇒ PD2 = a2 – c2 ...(i)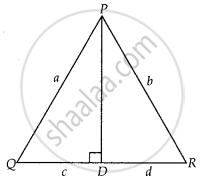
In right angled ∆PDR,
PR2 = PD2 + DR2 ...[By pythagoras theorem]
⇒ b2 = PD2 + d2
⇒ PD2 = b2 – d2 ...(ii)
From equations (i) and (ii),
a2 – c2 = b2 – d2
⇒ a2 – b2 = c2 – d2
⇒ (a – b)(a + b) = (c – d)(c + d)
Hence proved.
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 6 cm, 8 cm and 10 cm, respectively, then determine whether the triangle is a right angle triangle or not.
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
