Advertisements
Advertisements
प्रश्न
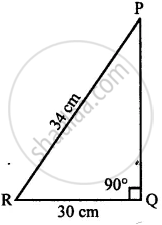
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
उत्तर
Given:
PR = 34 cm
QR = 30 cm
PQ =?
∠PQR = 90°
According to Pythagoras Theorem,
(PR)2 = (PQ)2 + (QR)2
(34)2 = PQ2 + (30)2
1156 = PQ2 + 900
1156 − 900 = PQ2
256 = PQ2
∴ PQ = `sqrt256` = 16 cm
APPEARS IN
संबंधित प्रश्न
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
The perimeter of the rectangle whose length is 60 cm and a diagonal is 61 cm is ______.
