Advertisements
Advertisements
प्रश्न
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
उत्तर
let O be the foot of the ladder. Let AO be the position of the ladder when it touches the window at A which is 9m high and CO be the position of the ladder when it touches the window at C which is 12m high.
Using Pythagoras theorem,
In ΔAOB,
BO2 = AO2 - AB2
BO2 = (15m)2 - (9m)2
BO2 = 225m2 - 81m2
BO2 = 144m2
BO2 = (12m)2
BO2 = 12m
Using Pythagoras theorem in ΔCOB,
DO2 = CO2 - CD2
DO2 = (15m)2 - (12m)2
DO2 = 225m2 - 144m2
DO2 = 81m2
DO = 9m
Width of the street
= DO + BO
= 9m + 12m
= 21m.
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
Find the value of (sin2 33 + sin2 57°)
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
In the given figure, angle ACB = 90° = angle ACD. If AB = 10 m, BC = 6 cm and AD = 17 cm, find :
(i) AC
(ii) CD

The foot of a ladder is 6m away from a wall and its top reaches a window 8m above the ground. If the ladder is shifted in such a way that its foot is 8m away from the wall to what height does its tip reach?
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
Find the unknown side in the following triangles
Find the length of the support cable required to support the tower with the floor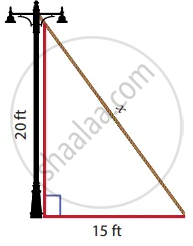
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
