Advertisements
Advertisements
प्रश्न
In ∆ABC, ∠BAC = 90°, seg BL and seg CM are medians of ∆ABC. Then prove that:
4(BL2 + CM2) = 5 BC2

उत्तर
Given: Δ ABC right angled at A, i.e., A = 90, where BL and CM are the medians.
To Prove: 4(BL2 + CM2) = 5BC2
Proof:
Since BL is the median,
AL = CL = `1/2` AC ...(1)
Similarly, CM is the median
AM = MB = `1/2`AB ...(2)
∴ by Pythagoras theorem,
(Hypotenuse)2 = (Height)2 + (Base)2 ...(3)
In ΔBAC,
(BC)2 = (AB)2 + (AC)2 ...(4)
∠BAC = 90°
In ΔBAL,
(BL)2 = AB2 + AL2 ...(From 1)
BL2 = AB2 + `(("AC")/2)^2`
BL2 = AB2 + `("AC"^2/4)`
Multiply both sides by 4,
4BL2 = 4AB2 + AC2 ...(5)
In ΔMAC,
CM2 = AM2 + AC2 ...(From 2)
CM2 = `(("AB")/2)^2` + AC2
CM2 = `("AB")^2/4` + AC2
Multiply both sides by 4,
4CM2 = AB2 + 4AC2 ...(6)
Adding 5 and 6,
4BL2 + 4CM2 = (4AB2 + AC2) + (AB2 + 4AC2)
4(BL2 + CM2) = 5AB2 + 5AC2
∴ 4(BL2 + CM2) = 5BC2
Hence, proved.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Identify, with reason, if the following is a Pythagorean triplet.
(4, 9, 12)
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.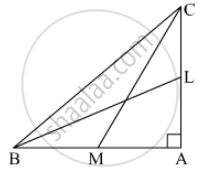
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
